Core functions¶

Core functions.

permute.core.corr(x, y, alternative='greater', reps=10000, seed=None, plus1=True)[source]¶

Simulate permutation p-value for Pearson correlation coefficient

Parameters

xarray-like
yarray-like
alternative{‘greater’, ‘less’, ‘two-sided’}: The alternative hypothesis to test
repsint
seedRandomState instance or {None, int, RandomState instance}: If None, the pseudorandom number generator is the RandomState instance used by np.random; If int, seed is the seed used by the random number generator; If RandomState instance, seed is the pseudorandom number generator
plus1bool: flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

tuple: Returns test statistic, p-value, simulated distribution

permute.core.one_sample(x, y=None, reps=100000, stat='mean', alternative='greater', keep_dist=False, seed=None, plus1=True)[source]¶

One-sided or two-sided, one-sample permutation test for the mean, with p-value estimated by simulated random sampling with reps replications.

Alternatively, a permutation test for equality of means of two paired samples.

Tests the hypothesis that x is distributed symmetrically symmetric about 0 (or x and y have the same center) against the alternative that x comes from a population with mean

greater than 0 (greater than that of the population from which y comes), if side = ‘greater’
less than 0 (less than that of the population from which y comes), if side = ‘less’
different from 0 (different from that of the population from which y comes), if side = ‘two-sided’

If keep_dist, return the distribution of values of the test statistic; otherwise, return only the number of permutations for which the value of the test statistic and p-value.

Parameters

xarray-like

Sample 1

yarray-like

Sample 2. Must preserve the order of pairs with x. If None, x is taken to be the one sample.

repsint

number of repetitions

stat{‘mean’, ‘t’}

The test statistic. The statistic is computed based on either z = x or z = x - y, if y is specified.

If stat == ‘mean’, the test statistic is mean(z).
If stat == ‘t’, the test statistic is the t-statistic– but the p-value is still estimated by the randomization, approximating the permutation distribution.
If stat is a function (a callable object), the test statistic is that function. The function should take a permutation of the data and compute the test function from it. For instance, if the test statistic is the maximum absolute value, 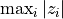$\max_i |z_i|$ , the test statistic could be written:

f = lambda u: np.max(abs(u))

alternative{‘greater’, ‘less’, ‘two-sided’}

The alternative hypothesis to test

keep_distbool

flag for whether to store and return the array of values of the irr test statistic

seedRandomState instance or {None, int, RandomState instance}

If None, the pseudorandom number generator is the RandomState instance used by np.random; If int, seed is the seed used by the random number generator; If RandomState instance, seed is the pseudorandom number generator

plus1bool

flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

float: the estimated p-value
float: the test statistic
list: The distribution of test statistics. These values are only returned if keep_dist == True

permute.core.spearman_corr(x, y, alternative='greater', reps=10000, seed=None, plus1=True)[source]¶

Simulate permutation p-value for Spearman correlation coefficient

Parameters

xarray-like
yarray-like
alternative{‘greater’, ‘less’, ‘two-sided’}: The alternative hypothesis to test
repsint
seedRandomState instance or {None, int, RandomState instance}: If None, the pseudorandom number generator is the RandomState instance used by np.random; If int, seed is the seed used by the random number generator; If RandomState instance, seed is the pseudorandom number generator
plus1bool: flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

tuple: Returns test statistic, p-value, simulated distribution

permute.core.two_sample(x, y, reps=100000, stat='mean', alternative='greater', keep_dist=False, seed=None, plus1=True)[source]¶

One-sided or two-sided, two-sample permutation test for equality of two means, with p-value estimated by simulated random sampling with reps replications.

Tests the hypothesis that x and y are a random partition of x,y against the alternative that x comes from a population with mean

greater than that of the population from which y comes, if side = ‘greater’
less than that of the population from which y comes, if side = ‘less’
different from that of the population from which y comes, if side = ‘two-sided’

If keep_dist, return the distribution of values of the test statistic; otherwise, return only the number of permutations for which the value of the test statistic and p-value.

Parameters

xarray-like

Sample 1

yarray-like

Sample 2

repsint

number of repetitions

stat{‘mean’, ‘t’}

The test statistic.

If stat == ‘mean’, the test statistic is (mean(x) - mean(y)) (equivalently, sum(x), since those are monotonically related)
If stat == ‘t’, the test statistic is the two-sample t-statistic– but the p-value is still estimated by the randomization, approximating the permutation distribution. The t-statistic is computed using scipy.stats.ttest_ind
If stat is a function (a callable object), the test statistic is that function. The function should take two arguments: given a permutation of the pooled data, the first argument is the “new” x and the second argument is the “new” y. For instance, if the test statistic is the Kolmogorov-Smirnov distance between the empirical distributions of the two samples, 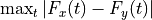$\max_t |F_x(t) - F_y(t)|$ , the test statistic could be written:

f = lambda u, v: np.max(
[abs(sum(u<=val)/len(u)-sum(v<=val)/len(v)) for val in np.concatenate([u, v])])

alternative{‘greater’, ‘less’, ‘two-sided’}

The alternative hypothesis to test

keep_distbool

flag for whether to store and return the array of values of the irr test statistic

seedRandomState instance or {None, int, RandomState instance}

plus1bool

flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

float: the estimated p-value
float: the test statistic
list: The distribution of test statistics. These values are only returned if keep_dist == True

permute.core.two_sample_conf_int(x, y, cl=0.95, alternative='two-sided', seed=None, reps=10000, stat='mean', shift=None, plus1=True)[source]¶

One-sided or two-sided confidence interval for the parameter determining the treatment effect. The default is the “shift model”, where we are interested in the parameter d such that x is equal in distribution to y + d. In general, if we have some family of invertible functions parameterized by d, we’d like to find d such that x is equal in distribution to f(y, d).

Parameters

xarray-like

Sample 1

yarray-like

Sample 2

clfloat in (0, 1)

The desired confidence level. Default 0.95.

alternative{“two-sided”, “lower”, “upper”}

Indicates the alternative hypothesis.

seedRandomState instance or {None, int, RandomState instance}

repsint

number of repetitions in two_sample

stat{‘mean’, ‘t’}

The test statistic.

If stat == ‘mean’, the test statistic is (mean(x) - mean(y)) (equivalently, sum(x), since those are monotonically related)
If stat == ‘t’, the test statistic is the two-sample t-statistic– but the p-value is still estimated by the randomization, approximating the permutation distribution. The t-statistic is computed using scipy.stats.ttest_ind
If stat is a function (a callable object), the test statistic is that function. The function should take two arguments: given a permutation of the pooled data, the first argument is the “new” x and the second argument is the “new” y. For instance, if the test statistic is the Kolmogorov-Smirnov distance between the empirical distributions of the two samples, 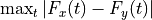$\max_t |F_x(t) - F_y(t)|$ , the test statistic could be written:

f = lambda u, v: np.max(
[abs(sum(u<=val)/len(u)-sum(v<=val)/len(v)) for val in np.concatenate([u, v])])

shiftfloat

The relationship between x and y under the null hypothesis.

If None, the relationship is assumed to be additive (e.g. x = y+d)
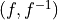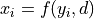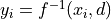
A tuple containing the function and its inverse $(f, f^{-1})$ , so $x_i = f(y_i, d)$ and $y_i = f^{-1}(x_i, d)$

plus1bool

flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

tuple: the estimated confidence limits

Notes

xtolfloat: Tolerance in brentq
rtolfloat: Tolerance in brentq
maxiterint: Maximum number of iterations in brentq

permute.core.two_sample_core(potential_outcomes_all, nx, tst_stat, alternative='greater', reps=100000, keep_dist=False, seed=None, plus1=True)[source]¶

Main workhorse function for two_sample and two_sample_shift

Parameters

potential_outcomes_allarray-like: 2D array of potential outcomes under treatment (1st column) and control (2nd column). To be passed in from potential_outcomes
nxint: Size of the treatment group x
repsint: number of repetitions
tst_stat: function: The test statistic
alternative{‘greater’, ‘less’, ‘two-sided’}: The alternative hypothesis to test
keep_distbool: flag for whether to store and return the array of values of the test statistic. Default is False.
seedRandomState instance or {None, int, RandomState instance}: If None, the pseudorandom number generator is the RandomState instance used by np.random; If int, seed is the seed used by the random number generator; If RandomState instance, seed is the pseudorandom number generator
plus1bool: flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

float: the estimated p-value
float: the test statistic
list: The distribution of test statistics. These values are only returned if keep_dist == True

permute.core.two_sample_shift(x, y, reps=100000, stat='mean', alternative='greater', keep_dist=False, seed=None, shift=None, plus1=True)[source]¶

One-sided or two-sided, two-sample permutation test for equality of two means, with p-value estimated by simulated random sampling with reps replications.

Tests the hypothesis that x and y are a random partition of x,y against the alternative that x comes from a population with mean

greater than that of the population from which y comes, if side = ‘greater’
less than that of the population from which y comes, if side = ‘less’
different from that of the population from which y comes, if side = ‘two-sided’

If keep_dist, return the distribution of values of the test statistic; otherwise, return only the number of permutations for which the value of the test statistic and p-value.

Parameters

xarray-like

Sample 1

yarray-like

Sample 2

repsint

number of repetitions

stat{‘mean’, ‘t’}

The test statistic.

If stat == ‘mean’, the test statistic is (mean(x) - mean(y)) (equivalently, sum(x), since those are monotonically related)
If stat == ‘t’, the test statistic is the two-sample t-statistic– but the p-value is still estimated by the randomization, approximating the permutation distribution. The t-statistic is computed using scipy.stats.ttest_ind
If stat is a function (a callable object), the test statistic is that function. The function should take two arguments: given a permutation of the pooled data, the first argument is the “new” x and the second argument is the “new” y. For instance, if the test statistic is the Kolmogorov-Smirnov distance between the empirical distributions of the two samples, 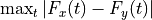$\max_t |F_x(t) - F_y(t)|$ , the test statistic could be written:

f = lambda u, v: np.max(
[abs(sum(u<=val)/len(u)-sum(v<=val)/len(v)) for val in np.concatenate([u, v])])

alternative{‘greater’, ‘less’, ‘two-sided’}

The alternative hypothesis to test

keep_distbool

flag for whether to store and return the array of values of the irr test statistic

seedRandomState instance or {None, int, RandomState instance}

shiftfloat

The relationship between x and y under the null hypothesis.

A constant scalar shift in the distribution of y. That is, x is equal in distribution to y + shift.
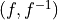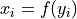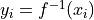
A tuple containing the function and its inverse $(f, f^{-1})$ , so $x_i = f(y_i)$ and $y_i = f^{-1}(x_i)$

plus1bool

flag for whether to add 1 to the numerator and denominator of the p-value based on the empirical permutation distribution. Default is True.

Returns

float: the estimated p-value
float: the test statistic
list: The distribution of test statistics. These values are only returned if keep_dist == True